理論ベースでパーティクルフィルタについて解説【実例あり】

2024/7/31

Category : 制御工学ロボティクス

本記事ではパーティクルフィルタの理論や背景知識についてを解説します。

なるべく理論ベースに徹しています。抽象性を保つことで、読者の方が何がパーティクルフィルタの本質で、どこからが実問題へのフィッティングになるのかを明瞭にわかりやすくする狙いがあります。

1. はじめに
- 前提
2. パーティクルフィルタが利用できるケース
3. パーティクルとは
4. パーティクルフィルタのアルゴリズム
5. リサンプリング
6. リサンプリングをする指標：有効サンプルサイズ
7. 実際に動かしてみる
8. おわりに
参考文献

1. はじめに

フィルタリングとはもともとは信号形成の目的で始まりました。予めこんな波形が来るはずだと微分方程式で表現されたモデルと実際に通報者から得られた信号波形から、本当はどんな情報を伝達したかったのかを知るという代物でした。

そんな波形整形の始まりは米国の数学者ノーバート・ウィーナーによるウィーナーフィルターに始まり、その後改良されたカルマンフィルタが登場。

カルマンフィルタはこちらも線形空間でしか用いることのできないものでしたが、アポロ計画でロケットの自己位置推定に用いられたことで知られます。

パーティクルフィルタはカルマンフィルタと同時期に誕生し、非線形空間でも利用でき、実装が簡単という代物でしたが、計算資源を消費することから2010年代になってようやく実用化され始めた経緯があるそうです。

例えばメディアンフィルタを用いることで多少のノイズは吸収できるでしょうが、しかし外れ値を含んでしまうのであって弾くわけではありません。

そんなときにパーティクルフィルタを用いれば、主に外れ値に対して極めて強い整形を期待する事ができます。

前提

対象となる読者はロボットのSLAMや信号形成(金融データなど)の応用にパーティクルフィルタを利用したいという方です。より数学的にアルゴリズムの学習を行いたいという方は英語の本になりますが、Beyond the Kalman Filterを強くおすすめします。日本円で30000円を超える本ですが、学習者にとって非常に有益な内容を提供してくれます。

また、本記事で紹介するパーティクルフィルタはBeyond the Kalman Filter中に紹介される”generic Particle Filter(一般的なパーティクルフィルタ)“であることを暗黙的に認めています。

2. パーティクルフィルタが利用できるケース

モデルがマルコフ過程で、不可観測(部分可観測)である場合に利用される手法です。といってもなんのことやらと思う方もいらっしゃるかも知れません。

マルコフ過程とは、時刻 $t$ における状態 $S_t$ が,ある行動の後に $S_{t+1}$ に遷移するモデルのことを言います。もし貴方が情報科出身ならオートマトンを思い浮かべるかも知れません。オートマトンに時系列要素が入ったものと言う感じの理解でよろしいと思います。

不可観測とはその名の通り、状態変数を直接観測できないことを言います。パーティクルフィルタにかける場合は、その中でも部分可観測である問題を扱います。部分可観測とは状態変数の一部が観測できることを指し、これは一部の変数が見えない場合やノイズが乗っていてそのままでは使えないなどのケースが該当します。

よくロボットの自己位置推定で用いるのには,ロボットの座標の観測が部分可観測である事が背景にあります。そもそも完全に観測できるモデルなら、その観測値が絶対に正しいわけですからそのまま観測値を採用すれば良いはずですよね。

3. パーティクルとは

パーティクルは日本語で粒子と言い、粒子をたくさん用意してシミュレーションをしてその結果の代表値(平均や中央値など)を取るのがパーティクルフィルタです。

パーティクルは

\left\{ \begin{matrix} S_t &&(状態変数)\\ W_t && (重み) \end{matrix} \right.

の２つの要素で定義されます。 $S_t$ は時刻 $t$ における「状態変数」のことを指し、ベクトルの場合もあります。例えばロボットではロボットの進行速度と向いている方角などで表現しますよね。

$W_t$ はパーティクルの持つ「重み」というもので、これは言い換えるとそのパーティクルがどの程度信用できるものかを表しています。「尤度」という言い方もされます。

4. パーティクルフィルタのアルゴリズム

パーティクルフィルタのアルゴリズムは予想と観測の2つの分布と、リサンプリングという工程からなります。 (これはベイジアンフィルタの思想が背景にあります。詳細はこちらの記事で解説しています)

予想分布(もしくは提案分布とも言います)は現在までの状態 $S_{1:t}$ と現在までの観測 $y_{1:t}$ を用いて表す、次の時刻における状態 $S_{t+1}$ の分布です。式で表すと

予想分布 \sim p\left(S_{t+1} | S_{1:t},y_{1:t}\right)

のように表現されます。これは高校数学でも見覚えのある条件付き確率というものですね。現在までの状態と観測があったとき、未来の状態はどのようになるかを表現しています。

次に観測値を用いて予想された値がどの程度信頼できるかを表現します。

重み \sim h\left(y_{1:t+1} | S_{1:t+1},y_{1:t}\right)

これも条件付き確率ですね！

ただしこれら２つの分布はベイジアン的な確率論から来ていることに注意してください。(古典的な頻度主義として捉えないでくださいね)

なおこのままではパーティクルフィルタは時間に比例してメモリを消費することになりますが、 $S_{t+1}$ は $S_t$ のみによって定まると仮定すれば、保持するパーティクルは現時刻のみで良いという特徴があります。実際に使用されるケースでは現時刻のみを保持するものが多いようです。

以下にPythonっぽいコードを記述します。

# パーティクルをM個,時系列データ長をTとする.

P = Particle[M]
for t in range(T): 
    for i in range(M):
      # パーティクルの持つ状態変数
      P[i].S = p(P.S , y[t])
      # パーティクルの重み
      P[i].W = h(P.S,y[t + 1])
    # 必要ならリサンプリングする
    if getESS() < threshold:
        P.resampling()
  # ここでは重み付き平均値をフィルタリング結果として採用する。
  for p in P:
      sum += p.S * p.W
  ans.append(sum//M)
return ans

5. リサンプリング

時刻が変遷していくとパーティクルの重みに偏りが出てきます。

重みが小さいパーティクルをいつまでも残していても推論の質を下げるだけですし、少ない数のパーティクルに高い信頼を置いてしまっては間違った推論を信じてしまうかも知れません。

そこで行われるのがリサンプリングです。リサンプリングは重みの小さいパーティクルを削除し、重みの大きいパーティクルを増やす手続きのことを指します。

(リサンプリング手法についての解説はこちらで行っています)

6. リサンプリングをする指標：有効サンプルサイズ

リサンプリングはしなければパーティクルの精度を落とすという話をしました。では常に行えばよいかと言うと、そうでもありません。それでは重みを用いる意味が失われてしまいます。

リサンプリングはし過ぎてもしなさ過ぎても良くないのです。

ではどんなタイミングで行えばよいのか？これを決める指標に「有効サンプルサイズ」というものがあります。これはパーティクルの重みがどの程度偏っているかを表す数値であり、

ESS(有効サンプルサイズ) = \frac{1}{\sum{W_{i}^{2}}}

として表されます。ただしここでの重みは総和が1になるように正規化済みのものとします。もし重みが理想的に均等な状態ならパーティクルの総数に漸近し、反対に偏る場合は小さくなります。

ESSに適当な閾値を設け、それを下回ったらリサンプリングを開始するようにすると良いでしょう。

7. 実際に動かしてみる

以下は今回形成する波形と形成後の波形です。

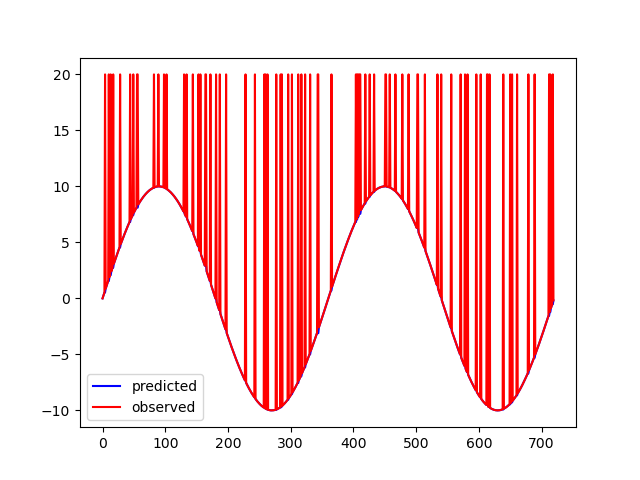
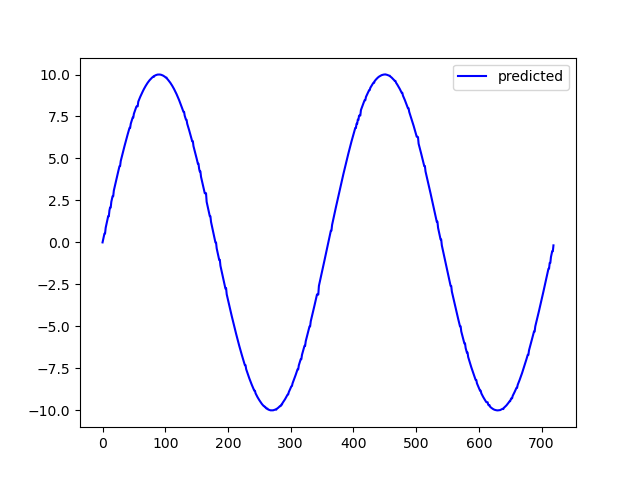
これはsin関数にランダムな位相で値を発散させた例です。(実際は2倍の振幅としました)明らかに誤った観測値ですよね。

これをフィルタリングした結果が右の波形です。きちんと整形できていると思います。

さて、パーティクルフィルタの設計にはモデルの状態変数、更新に必要な予想分布、重み導出に必要な尤度分布を与える必要があります。

まずパーティクルの状態変数ですが、今回は縦軸の値の1変数のみとしました。

次に予想分布ですが、今回使用したのは最も簡単な予想分布である恒等写像です。これは

S_{t+1} = S_t

としてしまうというものです。最も単純な設計ですが、こうすることで突飛な観測値を弾く事ができます。

また今回使用する尤度は平均を観測値、分散を適当に0.1と置いた正規分布としました。これは特に意味はありません。

\mathcal{N}\left(y_t,0.1\right)

以下は実際に使用したコードです。出力結果は

観測値 , パーティクルフィルタ後の値

という形になります。

#include <iomanip>
#include <vector>
#include <cmath>
#include <iostream>
#include <random>
#include <cstdlib>
using namespace std;
// パーティクル
class Particle{
    public:
        double theta;
        double weight;
        Particle(){
            this->theta = 0;
            this->weight = 0;
        }
        Particle(double theta,double weight){
            this->theta = theta;
            this->weight = weight;
        }
};
//パーティクルフィルタ
class ParticleFilter{
    public:
        ParticleFilter(vector<double> observations,int num_particles,double noise,double sigma, double threshold){
            this-> observations = observations;
            this->noise = noise;
            this->sigma = sigma;
            this->threshold = threshold;
            this->num_particles = num_particles;
            this->particles.resize(num_particles);
        };
        ~ParticleFilter(){
            observations.clear();
            particles.clear();
        }
        //フィルタリング結果を返す関数
        vector<double> estimate(){
            vector<double> result(observations.size());
            init();
            double sum = 0;
            for(int t = 0;t < observations.size();t++){
                double theta = 0;
                cout<<"time : "<<t<<"/"<<observations.size()<<endl;
                update(t);
                resample();
                normalize();
                for(int i = 0;i < num_particles;i++){
                    theta += this->particles[i].theta * this->particles[i].weight;
                }
                result[t] = theta;
            }
            cout<<resample_count<<endl;
            return result;
        }
    private:
        int resample_count = 0;
        vector<double> observations;
        vector<Particle> particles;
        double noise;
        double sigma;
        double threshold;
        int num_particles;
        random_device seed_gen;
        default_random_engine engine{seed_gen()};
    
        void init(){
            cout<<"initialize"<<endl;
            for(int i = 0;i < num_particles;i++){
                this->particles[i].theta = this->observations[0] + (rand() % 1000)/1000.0 * this->noise;
                this->particles[i].weight = 1.0/num_particles;
            }
            
        }
        //重みの算出に用いる
        double likelihood(Particle p,double obs){
            double mu = obs;
            double sigma = this->sigma;
            double x = p.theta;
            //標準正規分布
            double prob  = 1.0/(sqrt(2*M_PI*sigma*sigma))*exp(-0.5*(x-mu)*(x-mu)/(sigma*sigma)) + 1e-9;
            return prob;
        }
        //予想分布
        double predict(int i,int t){
            normal_distribution<double> dist(0,this->noise);
            double predict = this->particles[i].theta;
            //乱数を加え、少し移動させている。
            predict += dist(engine);
            return predict;
        }
        //パーティクルの更新
        void update(int t){
            for(int i = 0;i < num_particles;i++){
                this->particles[i].theta = predict(i,t);
                //尤度における予想値と観測値の信頼の重み割合。0~1の大きさで、1のときは観測値の重みが最大
                static const double parsent = 1;
                double mu = this->observations[t] * parsent + this->particles[i].theta * (1 - parsent);
                this->particles[i].weight = likelihood(this->particles[i],mu);
            }
        }
        //重みの正規化
        void normalize(){
            double sum = 0;
            for(int i = 0;i < num_particles;i++){
                sum += this->particles[i].weight;
            }
            for(int i = 0;i < num_particles;i++){
                this->particles[i].weight /= sum;
            }
        }
        //リサンプリングが必要かどうか
        bool need_resample(){
            // Effective Sample Size
            double sum = 0;
            for(int i = 0;i < num_particles;i++){
                sum += this->particles[i].weight * this->particles[i].weight;
            }
            double ess = 1.0/sum;
            return ess < threshold;
        }
        //リサンプリング(重要度重みリサンプリング)
        void resample(){
            if(!need_resample()){ return;}
            this->resample_count++;
            vector<Particle> new_particles;
            double max_weight = 0;
            for(int i = 0;i < num_particles;i++){
                max_weight = max(max_weight,this->particles[i].weight);
            }
            int index = rand() % num_particles;
            double beta = 0;
            for(int i = 0;i < num_particles;i++){
                beta += (rand() % 1000)/1000.0 * 2 * max_weight;
                while(beta > particles[index].weight){
                    beta -= particles[index].weight;
                    index = (index + 1) % num_particles;
                }
                new_particles.push_back(particles[index]);
            }
            this->particles.swap(new_particles);
        }
};

int main(int argc, char *argv[]){
    //引数にフィルタ後の波形を格納するファイルを渡す。
    if (argc != 2){
        cout<<"ERROR : please output file name"<<endl;
        return 1;
    }
    FILE *fp;
    if ((fp = fopen(argv[1],"w")) == NULL){
        cout<<"ERROR : cannot open file"<<endl;
        return 1;
    }
    random_device rnd;
    mt19937 mt(rnd());
    uniform_real_distribution<> rand(0,1);
    normal_distribution<> normal(0,0.1);
    vector<double> observations (360*2);
    double A = 10;//振幅
    //sin関数を獲得する
    for (int i = 0; i < observations.size(); i++){
        observations[i] = A *sin(i/180.0*M_PI);
        // 信号に誤りを加える
        if(rand(mt) < 0.1){
            observations[i] = A*2;
        }
    }
    ParticleFilter pf(observations,10000,1.0,0.1,0.5);
    cout<<"start"<<endl;
    vector<double> result = pf.estimate();
    // output.csvに書き込む
    for(int i = 0;i < result.size();i++){
        fprintf(fp,"%f,%f\n",observations[i],result[i]);
    }
    return 0;
}

8. おわりに

お疲れ様でした。以上で解説は終了となります。

パーティクルフィルタの強みが少しでも伝われば幸いです。

今回の実例では予想分布に恒等写像を使用しましたが、sin関数であると予めわかっているのなら当然sin関数を分布に使用したほうが良いでしょう。実際にいろいろなケースで試してみてください。

それではまた。

参考文献

国友直人,山本拓 “21世紀の統計学”
B Ristic, S Arulampalam ,N Gordon “Beyond the Kalman Filter: Particle Filters for Tracking Applications”
上田隆一 “詳解　確率ロボティクス　Pythonによる基礎アルゴリズムの実装”
足立修一, 丸田一郎 “カルマンフィルタの基礎”